A file manager does pretty much exactly what its name suggests; it allows you to manage files and folders from a graphical interface.
You can create, open, edit, view, play, move, copy, delete, rename, organize and otherwise manipulate files and folders to do your bidding, making use of a file manager.
In fact, you probably already use one every day, if you have any files at all. If not, you’re missing out. (Or maybe you always use the command line?)
Navigational file managers are the most common/popular. They allow you to move around the file system and view different directories and/or files in the same window, very much like a web browser.
Usually, the navigation options will include typing out locations, selecting locations from the navigation tree, opening new directories, pressing the Back and Forward buttons, etc.
Windows comes with a navigational file manager, set up and ready to run, called File Explorer (previously Windows Explorer, and still many times referenced as just Explorer).
How to Open File Explorer
File Explorer opens to “Computer” by most defaults, but will open to other locations based on the method used to open it. Try some out, until you find the method(s) that you prefer.
1. Click on the File Explorer Taskbar icon. (It will open to the Libraries location.)
2. Win + E (The keyboard shortcut combination of the Windows key and the letter E.)
3. Click on Start, then select your username, Document, Pictures, Music, or Computer from the list on the right-hand side.
4. Click on Start, then type in explorer.exe (it will fill out the search field) and hit Enter.
5. Create a shortcut of your favorite File Explorer location, and move the shortcut to your desktop, or any other handy location.
File Explorer Basics
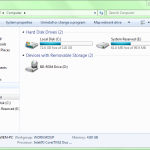If you’re familiar with using a browser, then using File Explorer will be simple.
A single-click will select an object (file, folder, etc.), and a double click will open it.
You have a back button, forward button, and an “Up One Level” button (pressing the Backspace key will do the same thing) up at the top, by default.
You can customize how the files are sorted and viewed, as well as open and otherwise manipulate them.
We’ll get into some of these standard file manipulation options in a later post; for now, let’s look at more File Explorer features and options.
The File Explorer Navigation pane
Once File Explorer is open, you will see a pane on the left called the Navigation pane, where your Favorites, Libraries, Computer, and Network are readily accessible.
You can navigate through your file system from within the Navigation pane.
Expand and collapse folders by clicking on the little arrows that show up next to them, until you find the location that you need.
When you click on a folder, it will be selected, and you will be moved to that folder location.
If for some reason, you dislike the Navigation pane (try it first, I think you’ll love it!), it can be removed by going to Organize > Layout and un-checking the Navigation pane. It will vamoose.
Other File Explorer Layout Options
If you explore the Organize > Layout section of File Explorer, you will find several options in addition to the Navigation pane.
The Details pane is that super-useful section down at the bottom of the window that displays all kinds of helpful information about an item if one is selected, or the number of items in your current location if nothing is selected.
The Preview pane shows up on the far right of the window, and give you a sneak peak into a file when it is selected.
The Library pane shows up just above the list of files/folders (when you are in a Library location) and displays the name of the Library location as well as the number of libraries included in the location and a shortcut option to “Arrange by”.
On the far right, just below the search field, there are three shortcuts that allow you to very quickly change your view, toggle the preview pane, and get help.
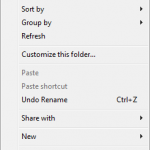For additional options, particularly in regards to viewing, arranging, sorting, creating new files, sharing, etc., right-click on empty space in your current window/location.
File Explorer Options
To adjust how File Explorer works (and doesn’t work), go to Organize > Folder and Search Options.
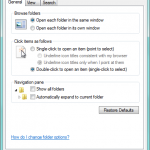In the General tab, you can make adjustment such as how folders are opened, how items are selected, and how you prefer your Navigation pane to work.
I prefer the default setting for each of these options.
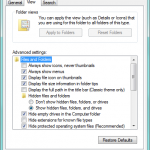The View tab allow you to toggle multiple options, many of which are rather intriguing. It’s worth reading through the options, at least, and maybe toggling a few to see if you like them.
I like to uncheck the “Hide extensions for known file types” option, so that I can always see file extensions, and know exactly what files I’m dealing with.
Another option that is good to uncheck is “Hide empty drives in the Computer folder”. Leaving it checked can lead to a lot of confusion the next time that you plug in an empty flash drive.
You can see all of the “secret” files, folders, and drives that Windows tries to keep out of your way, by selecting the “Show hidden files, folders, and drives” radio button option.
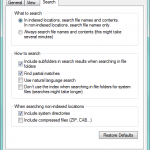The Search tab allows you to choose between several options that can make your file searches either more broad, or more refined. Use this with some care, or searches may end up taking too long!
Windows Libraries
Often, when File Explorer is opened, it opens to Libraries. While not a part of File Explorer itself, Libraries are very closely related, so this part will give you a brief idea of how they can be utilized.
There are several default Library folders (Documents, Music, Pictures, Videos) and you can create additional Libraries if needed.
The important part to remember, is that although you can put files in the Library folders, they are virtual folders that can show you (all together in one place) files that are scattered (stored) in all kinds of different locations around your computer/network/etc.
All you have to do is include other files/folders/locations/etc. This is easily done by right-clicking the folder that you want to include, and selecting Include in library and picking which Library to include the folder in.
If you have the Library pane enabled, you will be able to see how many locations are included when you are in each Library, and by clicking on the number of locations, you will be able to add/remove locations.
Summary
Hopefully with some of these basics in mind, you’ll be able to customize File Explorer to fit your individual needs.
If you are not a Windows-user, stay tuned for details about the Linux file explorer, Dolphin.